Hệ thập phân gồm 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 rất phổ biến trong xã hội của chúng ta ngày nay. 10 chữ số và cách ghi số theo-vị-trí có nguồn gốc từ đâu và được hoàn thiện như thế nào?
Ngày nay, các biểu tượng 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 phổ biến đến mức chúng ta hiếm khi biết ơn hệ thống chữ số này thật sự đặc biệt như thế nào. 15 thế kỷ phát triển đã trao cho chúng ta một phương pháp cô đọng để viết ra những con số rất lớn. Các chữ số của chúng ta có nguồn gốc từ hệ thống của các học giả Hindu ở Ấn Độ vào khoảng giữa thiên niên kỷ đầu tiên sau công nguyên. Hệ thống này được người Ả rập tiếp nhận và cuối cùng chuyển giao nó tới châu Âu vào thể kỷ 12. Vì lý do đó, các chữ số này còn được gọi là các chữ số Ả rập-Hindu.
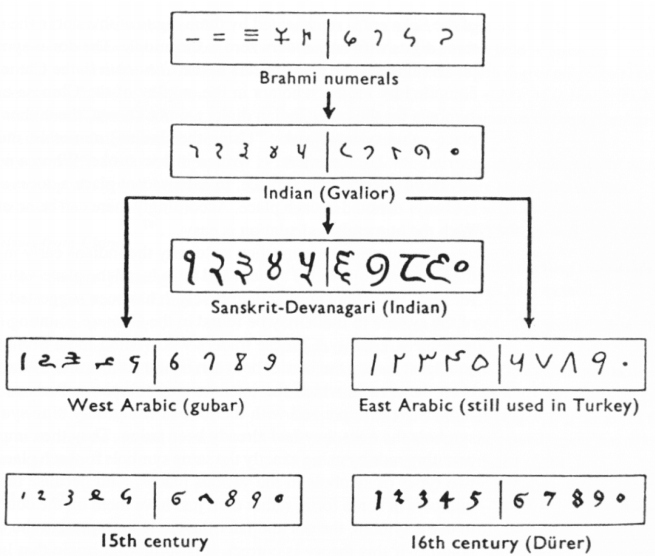
Chìa khóa cho sự thành công của hệ thống này là tính chất theo vị trí của nó. Chúng ta có tổng cộng mười ký hiệu để sử dụng, nhưng chắc chắn là chúng ta không bị giới hạn trong việc chỉ viết ra mười giá trị khác nhau. Một trong những điều đầu tiên mà tất cả chúng ta học ở trường là các con số được sắp xếp theo cột. Đọc từ phải sang trái, đầu tiên chúng ta có cột hàng đơn vị, cột hàng chục, cột hàng trăm, cột hàng ngàn và cứ thế. Vấn đề không chỉ là các ký hiệu chúng ta viết ra mà còn là vị trí chúng ta đặt chúng trong cách sắp xếp này. Đây là cái mà chúng ta gọi là một hệ thống số theo vị trí, giá trị của một chữ số tùy theo vị trí của nó (positional values).
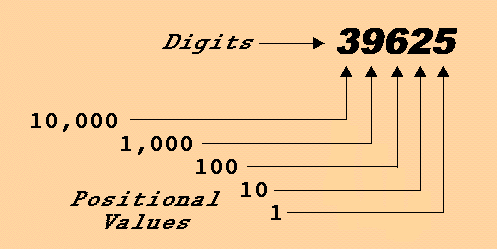
Vì sao hệ thống số theo vị trí lại xuất hiện từ thời nguyên thủy?
Khởi nguồn của việc dùng chữ số
Các hệ thống số sớm nhất phát sinh từ nhu cầu đếm của con người. Hệ thống cơ bản và ban sơ nhất trong tất cả những hệ thống đó là các dấu vạch (tally system), trong đó mỗi vật được đếm sẽ được ghi nhận bằng một dấu vạch trên trang giấy. Khi chúng ta đếm tới một con số lớn tương đối, trang giấy của chúng ta kết thúc bằng một tập hợp dài dằng dặc các dấu vạch không dễ nhìn cho lắm. Do đó, tổ tiên chúng ta bắt đầu các bước bổ sung như vạch một đường chéo qua bốn dấu thẳng đứng để tượng trưng cho số năm, và điều đó giải thích cho một ký hiệu số mới trong hệ thống của chúng ta.
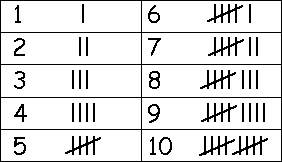
Giờ đây, nhìn lướt qua, ta thấy những con số mới có “ngoại hình” dễ coi hơn nhiều. Nhưng đến các số lớn hơn và lớn hơn nữa, một lần nữa chúng ta lại thấy các ký hiệu trở nên cồng kềnh. Một giải pháp cho vấn đề này là đưa thêm các ký hiệu mới. Đó chính xác là cách mà các hệ thống số được phát triển về mặt lịch sử.
Lấy ví dụ một hệ thống gồm các ký hiệu số khác nhau là hệ thống của người Babylon cổ. Hình 1 là bốn ký hiệu số đầu tiên:

Hệ thống này ban đầu được phát triển bởi người Sumer vào khoảng 3500 năm trước công nguyên nhưng nó luôn gắn liền với người Babylon.
(Người Sumer định cư ở phía Bắc Mesopotamia nằm giữa sông Tigris và Euphrates, ngày nay là Iraq)
Số 100 được biểu diễn bằng một ký hiệu duy nhất, một sự cải tiến lớn so với hệ thống dấu vạch ban đầu. Những con số lớn có hình dạng dấu vạch rất đáng sợ giờ đây có thể được minh họa một cách ngắn gọn hơn. Ví dụ số 3964 được viết như sau:
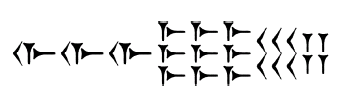
Người Babylon không quan tâm đến thứ tự các ký hiệu nhưng họ có khuynh hướng dùng một cách sắp xếp hợp lý: các ký hiệu giống nhau được nhóm lại và các nhóm được sắp xếp theo trật tự tăng dần, đọc từ phải sang trái.
Ngược lại với các chữ số Ả rập-Hindu, hệ thống số Babylon không tuân theo vị trí. Hình 3 và 4 là những ví dụ khác về những hệ thống số không theo vị trí. Hình 3 là chữ số của người Ai Cập, hình 4 là chữ số Minoan Linear B, loại chữ được cho là cổ nhất của người Hy Lạp:
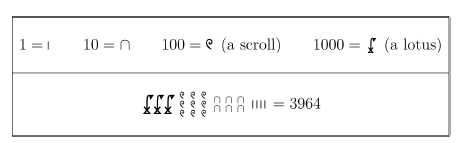
Các hệ số trong hình có vẻ dễ nhìn hơn trong mắt chúng ta so với hệ thống Babylon. Lý do có thể là vì họ chỉ dùng một ký hiệu cho mỗi số 100 và 1000, không như các ký hiệu phức tạp của người Babylon.
Dù vậy, tiếp theo chúng ta hãy tập trung vào hệ thống Babylon vì người Babylon sẽ tiếp tục giới thiệu một phát minh không bao giờ xảy ra với người Ai Cập hay người Hy Lạp (như chúng ta biết cho tới nay…!).
Hệ thống số theo vị trí của người Babylon
Người ta cho là người Babylon đã nhận ra những thiếu sót của hệ thống số không theo vị trí của họ. Họ có thể viết ra bất kỳ con số nào cho tới 9999 bằng các ký hiệu trong hình 1 nhưng không thể viết được số lớn hơn. Nếu họ muốn viết các số lớn tăng dần nữa, họ buộc phải đưa thêm nhiều ký hiệu mới. Điều này dẫn họ tới hai vấn đề: cách ký hiệu ngày càng công kềnh và cần phải nhớ nhiều ký hiệu.
Người Babylon cần một phương pháp khác để viết các số lớn.
Và phương pháp mới đó dĩ nhiên là hệ thống số theo vị trí.
Đầu tiên, họ loại bỏ tất cả ký hiệu ngoại trừ một và mười. Tiếp đến, họ sắp xếp các kết hợp những ký hiệu số này theo cột, đọc từ phải qua trái như chúng ta ngày nay. Tuy nhiên, hệ thống số Babylon không giống của chúng ta vì không phải là hệ thập phân mà là hệ lục thập phân (60), các cột kế tiếp nhau biểu diễn lũy thừa 60 thay vì 10. Chúng ta đã thừa kế hệ thống này để theo dõi thời gian và đo lường các góc, ví dụ 60 giây trong một phút.
Trong ví dụ sau, chúng ta sẽ vẽ thêm các đường biên quanh các cột cho rõ ràng (dù người Babylon không làm điều này). Cột có giá trị thấp nhất là cột ngoài cùng bên phải có bất kỳ con số nào lên tới 59-phiên bản lục thập phân của một cột đơn vị. Bất kỳ con số nào ít hơn hay bằng 59 cũng sẽ xuất hiện trong hệ thống này, ví dụ số 42 bên dưới.

Để đi xa hơn 59, chúng ta phải thêm một cột khác vào bên trái, cột này biểu diễn bội số của 60. Ví dụ số 60 của người Babylon:

Con số này biểu diễn (1 x 60) + (0 x 1) = 60 (ký hiệu trong cột bên phải chỉ ra một cột trống, chúng ta sẽ quay lại nó ngay).
Còn chuỗi ký hiệu này

biểu diễn con số (11 x 60) + (24 x 1) = 684.
Với một cột, giới hạn của chúng ta là 59, với hai cột ta có thể viết các số lớn tới (59 x 60) + (59 x 1) = 3599. Để đi xa hơn, chúng ta chỉ cần thêm các cột vào bên trái biểu diễn các bội số của lũy thừa cao hơn của 60 (602, 603…). Nếu chúng ta thêm cột thứ ba thì giá trị được nhập vào biểu diễn bội của 3600 = 60 x 60, và cột thứ tư biểu diễn bội của 603 = 216.000.
Với cách sắp xếp 3 cột, chúng ta có thể viết ra các con số lớn đến (59 x 3600) + (59 x 60) + (59 x 1) = 215.999. Trong thiết kế mới này, con số yêu thích của chúng ta 3964 sẽ trở thành:

bởi vì 3964 = (1 x 3600) + (6 x 60) + (4 x 1).
Dễ thấy rằng, chúng ta có thể mở rộng hệ thống này tới vô hạn chỉ bằng cách thêm nhiều cột vào bên trái. Chúng ta không còn cần thêm ký hiệu mới.
Có một ít điều nên nói về ký hiệu “-” được dùng để chỉ một cột trống trong cách biểu diễn hệ đếm 60.
Đầu tiên, người Babylon không có ký hiệu nào như thế. Họ chừa một chỗ trống để biểu thị một cột trống hoặc là họ không đánh dấu cột. Điều này làm cho các chữ số của họ trở nên mơ hồ.
Ví dụ, biểu tượng này
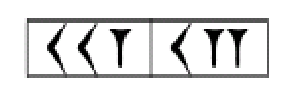
có thể ký hiệu cho một trong các số sau
(21 × 60) + (12 × 1) = 1.272
hoặc (21 × 3.600) + (12 × 1) = 75.612
hoặc (21 × 3.600) + (12 × 60) = 76.320
…
Tuy nhiên, dường như người Babylon không bao giờ gặp vấn đề ở đây bởi vì ý nghĩa con số luôn rõ ràng nhờ ngữ cảnh. Mãi cho tới khi người Ba Tư kế thừa hệ số Babylon vào khoảng năm 400 trước công nguyên thì mới có thêm một ký hiệu đánh dấu một cột để trống. Đó là ký hiệu
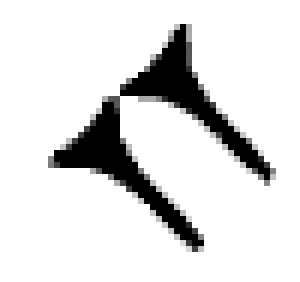
do đó, số 216.001 được viết thành

Sự chính xác của hệ thập phân
So với các hệ thống không theo vị trí, các hệ thống theo vị trí tương đối hiếm trong lịch sử. Tuy nhiên, lợi ích của việc tiếp nhận một hệ thống số theo vị trí rất rõ ràng: chúng chính xác hơn và dễ sử dụng hơn. Hệ thống của chính chúng ta đưa sự chính xác này tới tột cùng: thay vì dùng kết hợp các chữ số tạo nên giá trị ở mỗi vị trí, chúng ta chỉ có đúng một ký hiệu cho mỗi vị trí. Dễ thấy vì sao người Babylon không dùng cách này cho chính họ: tổng cộng họ sẽ cần tới 60 ký hiệu, vì vậy hệ thống số của họ sẽ khó nhớ.
Hệ thống “một ký hiệu mỗi vị trí” của chúng ta có nghĩa là các chữ số của chúng ta chính xác tới hết mức mà chúng có thể. Hãy so sánh cách viết 9.876.543.210 của chúng ta với cách của người Babylon:

Tuy vậy, các chữ số Ả rập-Hindu cũng có nhược điểm của chúng.
Tất cả các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 đều là các ký hiệu trừu tượng vốn không có hoặc rất ít liên quan tới các số lượng mà chúng biểu diễn, khác với sự liên tưởng mà chúng ta áp đặt lên chúng. Cách viết số “hai” kiểu Babylon dễ kết nối với số lượng hai hơn là ký hiệu 2 về mặt trực quan. Để làm số học trong các chữ số chúng ta, chúng ta phải quen với các quy tắc phép toán của chúng.
Chúng ta phải biết khi thêm ký hiệu 1 vào ký hiệu 2, chúng ta được ký hiệu 3 v.v… Chúng ta cần biết bảng cửu chương. Chúng ta cần biết khi chúng ta thêm 1 vào 9 trong một cột cụ thể thì chúng ta cần nhập 0 vào cột đó và thêm 1 vào cột kế bên bên trái.
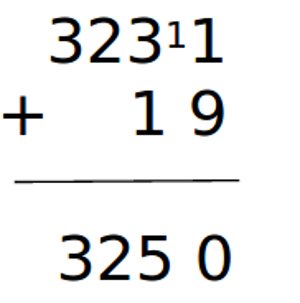
Khi được liệt kê như thế này, các quy tắc bắt đầu có vẻ phức tạp đối với những người quan sát bên ngoài không có sẵn kiến thức về hệ thống chữ số của chúng ta.
Dẫu sao thì, sau những lời khen ngợi sự kỳ diệu của các hệ thống số theo vị trí, tôi (tác giả Christopher) không muốn làm giảm giá trị của các chữ số của chúng ta. Sự thật là chúng ta thấy chúng dễ dùng, dù đó là vì chúng ta đã được hướng dẫn dùng chúng từ tuổi nhỏ, hay là vì chúng vốn có tính dễ dùng, ít nhất là khi xem xét từ quan điểm thực dụng.
Trong thực tế, các chữ số này quá phổ biến (phổ biến hơn nhiều so với sự phổ biến mà các chữ số Babylon đã từng có), đến mức mà việc thay đổi chúng là điều cực kỳ khó với chúng ta, kể cả khi chúng ta muốn. Giống như là chúng đã có sẵn ở đây!
Vì vậy, lần kế tiếp mà bạn kiểm tra số dư tài khoản ngân hàng hay gọi đến một số điện thoại nào đó, hãy dành 1 giây để suy nghĩ về hàng thế kỷ phát triển đã qua đi để sản sinh ra những ký hiệu vô giá.
Xem thêm một số bài viết khác về toán học: Tại Đây






