Các nhà toán học gần đây đã tiến được một bước gần hơn với mục tiêu “số mũ hai” của họ, tức là nhân một cặp ma trận cỡ nxn chỉ trong $n^2$ bước. Liệu họ có thể đạt được mục tiêu đó hay không?
Với các nhà khoa học máy tính và các nhà toán học, những đánh giá về “số mũ hai” là những kết quả quan trọng để ý thức về thế giới nên như thế nào?
“Thật khó để phân biệt tư duy khoa học với tư duy mơ mộng. Tôi muốn số mũ là hai vì nó đẹp.” – Chris Umans, Viện Công nghệ California cho biết: “Số mũ hai” đề cập đến ở đây là về tốc độ lý tưởng – về số bước cần thiết để thực hiện một trong những phép toán cơ bản nhất trong toán học: phép nhân ma trận. Nếu số mũ hai là có thể đạt được, ta có thể thực hiện phép nhân ma trận một cách nhanh nhất có thể về mặt vật lý. Còn nếu không, chúng ta đang mắc kẹt trong một thế giới có lẽ không phù hợp với giấc mơ của chúng ta.
Như chúng ta biết, ma trận là các mảng số. Khi có hai ma trận có kích thước tương thích, ta có thể nhân chúng để tạo ra ma trận thứ ba. Ví dụ: nếu bắt đầu với một cặp ma trận 2×2, ta sẽ tính được tích của chúng và kết quả cũng sẽ là ma trận 2×2, gồm 4 phần tử . Tổng quát hơn ta cũng có tích của một hai ma trận cỡ nxn cũng là một ma trận cỡ nxn với $n^2$ phần tử.
Chính vì lý do này, người ta hy vọng rằng ta có thể nhân các cặp ma trận cỡ nxn trong $n^2$ bước – tức là với số bước chỉ cần viết ra câu trả lời cho các phần tử của ma trận. Đây cũng là nơi xuất phát của “số mũ hai”.
Và trong khi không ai biết chắc liệu có thể đạt được điều đó hay không thì các nhà nghiên cứu vẫn tiếp tục đạt được những tiến bộ theo hướng này.
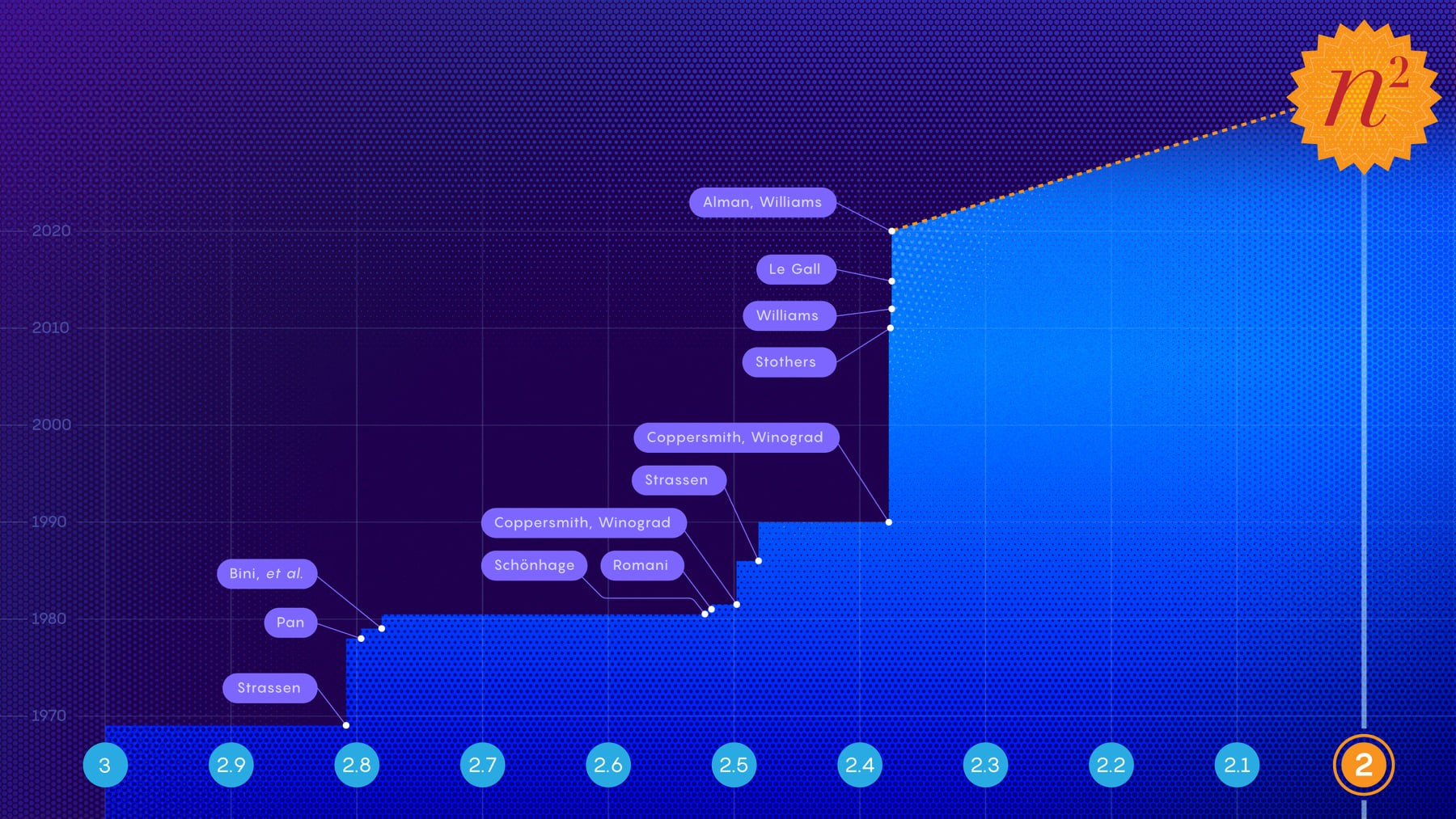
Một bài báo được đăng vào gần nhất vào tháng 10 năm 2020, mô tả phương pháp nhanh nhất từ trước đến nay để nhân hai ma trận với nhau. Kết quả là của Josh Alman , một nhà nghiên cứu sau tiến sĩ tại Đại học Harvard, và Virginia Vassilevska Williams thuộc Viện Công nghệ Massachusetts: sai lệch về số mũ đã giảm đi khoảng một phần trăm nghìn so với số mũ tốt nhất trước đó. Đó là điển hình của một trong những thành tựu gần đây trong lĩnh vực này.
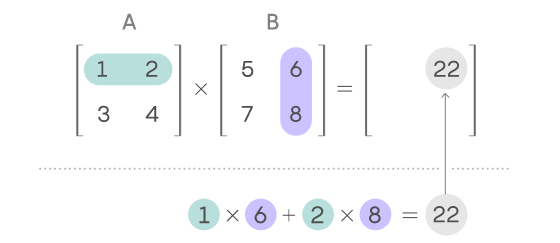
Để hiểu rõ quá trình và cách cải thiện quá trình này, ta hãy bắt đầu với một cặp ma trận 2×2, A và B. Khi tính toán từng phần tử của ma trận tích, ta sử dụng hàng tương ứng của A và cột tương ứng của B. Vì vậy, để có phần tử trên cùng bên phải, ta nhân số đầu tiên ở hàng đầu tiên của A với số đầu tiên ở cột thứ hai của B, sau đó nhân số thứ hai ở hàng đầu tiên của A với số thứ hai trong cột thứ hai của B, và cộng hai kết quả đó với nhau.
Thao tác này được gọi là lấy “tích trong” của một hàng với một cột. Để tính toán các phần tử khác trong ma trận tích, ta lặp lại quy trình với các hàng và cột tương ứng.Nhìn chung, phương pháp để nhân hai ma trận 2×2 này cần dùng đến 8 phép nhân với một số phép cộng và tổng quát hơn, theo cách này để nhân 2 ma trận cỡ nxn ta sẽ cần dùng tới $n^3$ phép nhân và một số phép cộng.
Tuy nhiên, khi ma trận với kích cỡ lớn hơn, số phép nhân cần dùng để tính tích của chúng tăng nhanh hơn nhiều so với số phép cộng. Trong khi ta cần 8 phép nhân trung gian để tìm tích của 2 ma trận 2×2, thì lại cần tới 64 phép nhân để tích của 2 ma trận 4×4. Số lượng phép cộng cần dùng để tính thì lại gần nhau hơn nhiều. Số phép cộng mà ta cần dùng bằng số lượng các phần tử trong ma trận tích, tức là cần 4 phép cộng với ma trận 2×2 và 16 với ma trận 4×4. Sự khác biệt giữa phép cộng và phép nhân này cũng giải thích lý do tại sao các nhà nghiên cứu thường sẽ đo tốc độ của phép nhân ma trận hoàn toàn dựa trên số lượng các phép nhân.
“Các phép nhân là tất cả,” Umans nói. “Số mũ trên thời gian chạy cuối cùng chỉ hoàn toàn phụ thuộc vào số phép nhân. Các phép cộng gần như là sẽ biến mất. “
Trong nhiều thế kỷ, người ta nghĩ rằng $n^3$ đơn giản là thời gian nhanh nhất mà ta có thể thực hiện được. Vào năm 1969, Volker Strassen được cho là đã chứng minh rằng không có cách nào để nhân ma trận 2×2 bằng cách sử dụng ít hơn 8 phép nhân. Nhưng rõ ràng anh ta không thể tìm được cách chứng minh, và sau một thời gian anh ta nhận ra rằng: Thực ra có một cách để làm điều đó với 7!
Strassen đã đưa ra ý tưởng với một tập hợp các mối quan hệ phức tạp để có thể thay thế một trong 8 phép nhân đó bằng 14 phép cộng bổ sung. Điều đó nghe có vẻ không có nhiều khác biệt, nhưng nó dẫn đến những kết quả thành công nhờ tầm quan trọng của phép nhân so với phép cộng. Và bằng việc tìm ra cách để lưu một phép nhân đơn lẻ cho các ma trận nhỏ 2×2, Strassen đã tìm ra một lỗ hổng mà anh ta có thể khai thác được khi nhân các ma trận lớn hơn.Vassilevska Williams nói: “Cải tiến nhỏ này dẫn đến những cải tiến lớn với những ma trận lớn.”
Ví dụ: Giả sử ta muốn nhân một cặp ma trận 8×8. Một cách để làm điều đó là ta chia mỗi ma trận lớn thành bốn ma trận 4×4, khi đó 2 ma trận 8×8 ban đầu được coi như là 2 ma trận 2×2, ở đó mỗi ma trận 2×2 thì có 4 phần tử, mỗi phần tử là một ma trận 4×4. Thông qua một số thao tác này, ta lại có thể chia bản thân mỗi ma trận 4×4 thành bốn ma trận 2×2.
Ưu điểm của sự giảm thiểu này là liên tục chia nhỏ các ma trận lớn hơn thành các ma trận nhỏ hơn – là có thể áp dụng thuật toán Strassen lặp đi lặp lại cho các ma trận nhỏ hơn, và rõ ràng sẽ tiết kiệm được thời gian ở mỗi bước. Và thuật toán của Strassen đã cải thiện tốc độ của phép nhân ma trận từ $n^3$ thành $n^{2.81}$ phép tính nhân.
Cải tiến lớn tiếp theo là vào cuối những năm 1970, với một cách thức cơ bản là mới để tiếp cận vấn đề. Nó liên quan đến việc chuyển phép nhân ma trận thành một bài toán tính toán khác trong đại số tuyến tính liên quan đến các đối tượng được gọi là tensors. Các tensors đặc biệt được sử dụng trong bài toán này là các mảng ba chiều gồm nhiều phần khác nhau, mỗi phần trông giống như một bài toán nhân ma trận nhỏ.
Phép nhân ma trận và bài toán liên quan đến các tensors tương đương với nhau theo một nghĩa nào đó, nhưng các nhà nghiên cứu đã có các cách làm nhanh hơn để giải quyết bài toán sau. Điều này khiến họ phải xác định tỉ lệ tương ứng giữa hai ma trận: Bạn có thể nhân ma trận lớn đến mức nào để có cùng một chi phí tính toán mà nó cần để giải bài toán tensor?“
Đây là một mô hình rất phổ biến trong khoa học máy tính lý thuyết, về việc giảm bớt giữa các vấn đề để cho thấy chúng dễ hoặc khó như nhau,” Alman nói.
Năm 1981, Arnold Schönhage đã sử dụng phương pháp này để chứng minh rằng có thể thực hiện phép nhân ma trận với $n^{2.522}$ phép tính nhân. Strassen sau đó gọi cách tiếp cận này là “phương pháp laser”.
Trong vài thập kỷ qua, mọi cải tiến trong phép nhân ma trận đều đến từ những cải tiến trong phương pháp laser, do các nhà nghiên cứu đã tìm ra những giải pháp ngày càng hiệu quả để chuyển đổi giữa hai vấn đề. Trong chứng minh mới của họ, Alman và Vassilevska Williams đã giảm bớt mâu thuẫn giữa hai bài toán và cho thấy rằng có thể “mua” nhiều phép nhân ma trận hơn mức đã nhận ra trước đây để giải một bài toán tensor có kích thước nhất định.
Henry Cohn của Microsoft Research cho biết: “Về cơ bản Josh và Virginia đã tìm ra cách sử dụng máy móc bên trong phương pháp laser và điều chỉnh nó để thu được kết quả tốt hơn”.Bài báo đã cải thiện giới hạn tốc độ lý thuyết trên phép nhân ma trận thành $n^{2,3728596}$ .
Điều này giúp Vassilevska Williams “giành lại vương miện” trong cuộc đua về thời gian nhân ma trận, mà trước đó cô đã nắm giữ vào năm 2012 ( $n^{2,372873}$ ), sau đó bị mất vào năm 2014 vào tay François Le Gall ( $n^{2,3728639}$ ).
Tất nhiên câu chuyện giành lại vương miện chỉ là trò đùa nhưng rõ ràng cách tiếp cận này đang giảm dần thời gian tính toán. Trên thực tế, sự cải tiến của Alman và Vassilevska Williams có thể đã đạt được hiệu quả gần như tối đa của phương pháp laser – tuy còn thiếu xa so với mục tiêu lý tưởng cuối cùng.
“Không có khả năng có một bước nhảy vọt để tính lũy thừa hai bằng cách sử dụng phương pháp cụ thể này,” Umans nói.
Có lẽ để đạt được điều đó, chúng ta sẽ phải khám phá các phương pháp mới và duy trì niềm tin rằng điều đó là có thể. Và … biết đâu một ngày nào đó kì tích sẽ xuất hiện !?!
Bài viết tham khảo tại: https://www.quantamagazine.org/mathematicians-inch…/






