VTED.net giới thiệu đến các bạn đọc bài viết: Xây dựng tư duy trừu tường trong toán học bằng Epsilon- Delta
Khi tôi nhắm mắt và quay ngược thời gian, tôi thấy một sinh viên đại học đang ngồi ở hàng ghế sau và trông buồn bã trong khi vị giáo sư đang đứng cạnh chiếc bảng đen, viết các định nghĩa toán học lên đó bằng phấn. Tiếng click, click, click vẫn rõ ràng mỗi khi giáo sư viết lên bảng. Sau đó, sinh viên đi sâu vào suy nghĩ khi giáo sư nói:

Rồi một điều phi thường đã xảy ra vào một buổi tối mùa thu khi tôi đọc một cuốn sách giải thích ý nghĩa của nó. Sau khi đọc cuốn sách, tôi hoàn toàn hiểu epsilon có nghĩa là gì. Cuốn sách là “Người đàn ông chỉ yêu những con số: Câu chuyện của Paul Erdos và Cuộc tìm kiếm sự thật toán học.” Cuốn sách nói về Paul Erdös, nhà toán học vĩ đại, người đã gọi các con của mình là “epsilon.” Nó có vẻ khó xử, nhưng đó là lúc tôi nắm bắt được ý tưởng về epsilon. Epsilon đại diện cho một số lượng nhỏ của một con số, và nó không phải là một hằng số như trẻ em. Trẻ con thì ít, và chúng luôn thay đổi. Sau đó, tôi ngừng nguyền rủa khái niệm epsilon-delta, và tôi bắt đầu yêu thích nó. Học kỳ đó, tôi cũng đã vượt qua kỳ thi Giải tích, và tôi cảm thấy hạnh phúc về điều đó ngay cả hôm nay.
Đối với Galileo, một ông già đã nói “Thế mà nó vẫn di chuyển” ngay trước khi bị Giáo hội bắt giữ , cuốn sách về thiên nhiên dường như được viết bằng ngôn ngữ toán học. Galileo có thể đọc và hiểu ngôn ngữ toán học. Chúng ta biết điều này vì ông ấy là người duy nhất trong thế kỷ 16 biết rằng Trái đất chuyển động quanh Mặt trời và có can đảm chống lại giáo lý của Giáo hội và nói điều đó.
Những bộ óc thiên tài như Galileo đã khám phá ra toán học với tư duy của họ, và nó đã mở ra một vũ trụ hoàn toàn khác cho họ. Ngày nay đầu óc trẻ có thể gặp khó khăn để học ngôn ngữ đó, nhưng để hiểu ngôn ngữ toán học, điều kiện tiên quyết duy nhất là trí tò mò và trí tưởng tượng. Vì vậy, tư duy toán học là cần thiết để hiểu và sử dụng các ý tưởng.
Trên thực tế, con người luôn nghĩ đến việc nâng cao hiểu biết về môi trường của họ. Một điều, một sự việc xảy ra hoặc một từ có thể khiến chúng ta bắt đầu suy nghĩ. Hầu hết những suy nghĩ này đều liên quan đến tư duy toán học. Ví dụ, khi chúng ta nhìn thấy một nhóm đối tượng, chúng ta có thể muốn biết có bao nhiêu đối tượng.
Vì vậy, epsilon giống như bước đầu tiên để bắt đầu tư duy toán học hoặc trừu tượng sâu sắc. Nó chỉ là một biến khác như x hoặc n, và các nhà toán học sử dụng nó trong các bất đẳng thức đại số. Tuy nhiên, nó không giống như pi hoặc e và không thực sự có định nghĩa đầy đủ. Trong lý thuyết giới hạn, epsilon được sử dụng để biểu thị các số vô hạn gần bằng 0 nhưng không bằng 0. Vì vậy, chúng ta có thể nói epsilon là một “số thực dương nhỏ tùy ý”, và đây là điều quan trọng nhất mà chúng ta cần biết về epsilon. Nói cách khác, hãy nghĩ về một số dương chỉ lớn hơn 0 và nhỏ hơn tất cả các số dương và thay vì diễn đạt nó trong 10 giây mỗi lần, hãy gọi nó là “epsilon”. Nhân tiện, epsilon có thể bao gồm các số khác xa số 0 khi chúng ta cần. Không có gì sai về mặt toán học khi làm cho epsilon đại diện cho bất cứ thứ gì.
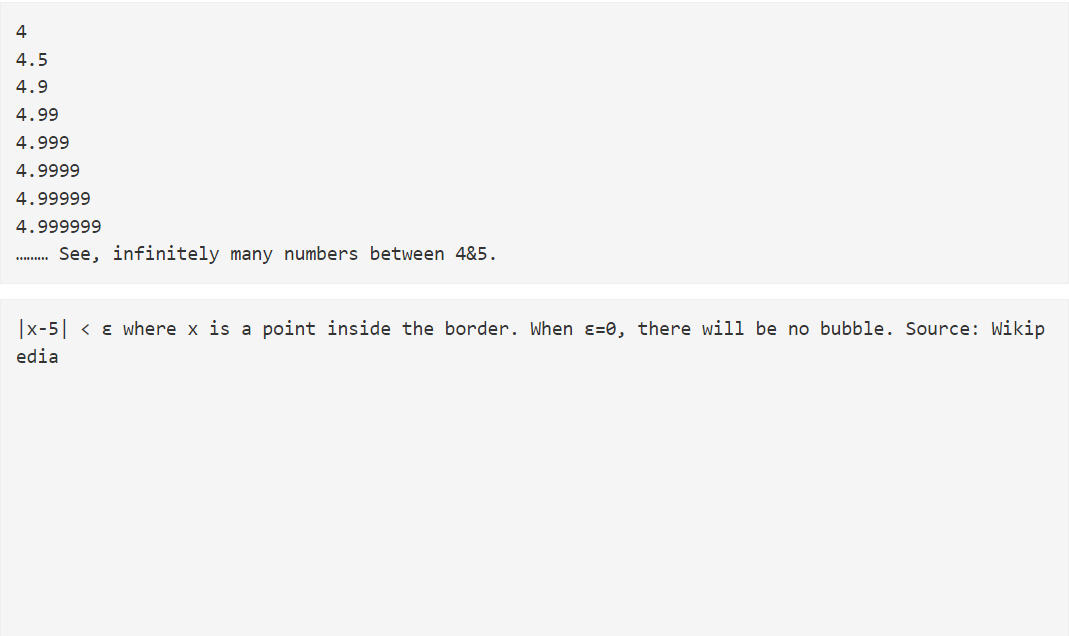
Chúng ta có thể hỏi nếu epsilon chỉ là một số hay nhiều số? Câu trả lời là hấp dẫn. Vâng, tất nhiên, nó chỉ là một con số, nhưng nó cũng không phải là một con số bất biến. Epsilon có thể đại diện cho tất cả các số dương. Ví dụ, nếu chúng ta nói 0,1 rất gần với 0 và gọi nó là epsilon, chúng ta đã nhầm vì 0,01 nhỏ hơn 0,1. Tuy nhiên, 0,01 không phải là số dương nhỏ nhất vì 0,001 nhỏ hơn 0,01.
Tương tự, 0,0001 nhỏ hơn 0,001 và 0,00001 nhỏ hơn 0,0001, v.v. Bạn có thể tiếp tục viết “0,000000000000…” cho đến khi bạn gần đạt đến một giá trị cực kỳ nhỏ. Thật không may, bạn vẫn sẽ không bao giờ nhận được số dương nhỏ nhất vì sẽ luôn có… 001… ngay sau số 0 cuối cùng của bạn nhỏ hơn số của bạn, giống như nghịch lý của Zeno . Vì vậy, chúng tôi sử dụng epsilon để biểu thị một số lượng nhỏ, giống như một lỗi.
Nói về Epsilon vẫn chưa hoàn thành trước khi chúng ta xem cách nó sử dụng trong giới hạn. Trong bài giảng đầu tiên về giới hạn, chúng ta thấy:

Điều thú vị là Leibniz và Newton chưa bao giờ sử dụng chứng minh epsilon-delta, những người gần như đồng thời và độc lập đã phát minh ra Máy tính nhiều năm trước. Chứng minh epsilon-delta lần đầu tiên được nhìn thấy trong các công trình của Cauchy, Résumé des leçons Sur le Calcul infinitésimal, gần 150 năm sau Leibniz và Newton.
Định nghĩa chính xác ở trên là về tính liên tục của một hàm. Ở đây, tính liên tục có nghĩa là chúng ta có thể vẽ đồ thị của một hàm số từ điểm x đến điểm a mà không cần nhấc bút chì lên. Trong một hàm liên tục, khi chúng ta cắm một giá trị, chúng ta luôn nhận được một đầu ra. Vì vậy, đối với các đầu vào “x và a”, chúng ta lấy “ f (x) và f (a) ” làm đầu vào. Khi chúng ta thực hiện khoảng cách | xa | nhỏ dần theo chiều ngang thì khoảng cách | f (x) – f (a) | sẽ nhỏ hơn và nhỏ hơn theo chiều dọc.
Hãy làm một ví dụ nhỏ.

Xem thêm một số bài viết khác về toán học: Tại Đây






